NFL Point Spread: 1978-2013

NFL (National Football League) point spread is a major focus point for those looking to place wagers on upcoming weekly games during the football season.

The point spread is a figure generated by an oddsmaker to equalize wagering between opponents, which in the NFL is a matchup between two teams – a favorite and an underdog. In the instance when a matchup does not have either a favorite or an underdog, the point spread is set at 0 and the game is designated as a “Pick’em.”

An example of a point spread in play is the September 5th, 2013 matchup between the Denver Broncos and the Baltimore Ravens, where the point spread was 7.5 points. The Denver Broncos were favored by 7.5 points and would go on to outscore the Baltimore Ravens 49 to 27. For wagers on the favored Denver Broncos, the score was adjusted to reflect 49 minus 7.5 for a final score of 41.5 for the Denver Broncos versus 27 for the Baltimore Ravens. For wagers on the underdog Baltimore Ravens, the score was adjusted to reflect 27 plus 7.5 for a final score of 34.5 for the Baltimore Ravens versus 49 for the Denver Broncos.

The data downloaded from Kaggle: NFL scores and betting data, contained an array of variables nested in a series of individual csv and xml files. This project’s sole focus centered around point spread. Therefore, only csv files with the title suffix “lines.csv” from the dataset were extracted for use.

After importing the data using the read_csv() function, the immediate efforts were centered on tidying the data using a number of functions - janitor::clean_names() to generate compatible variable names, mutate() to add columns, select() to focus on the variables of interest, and rename() to rename variables.

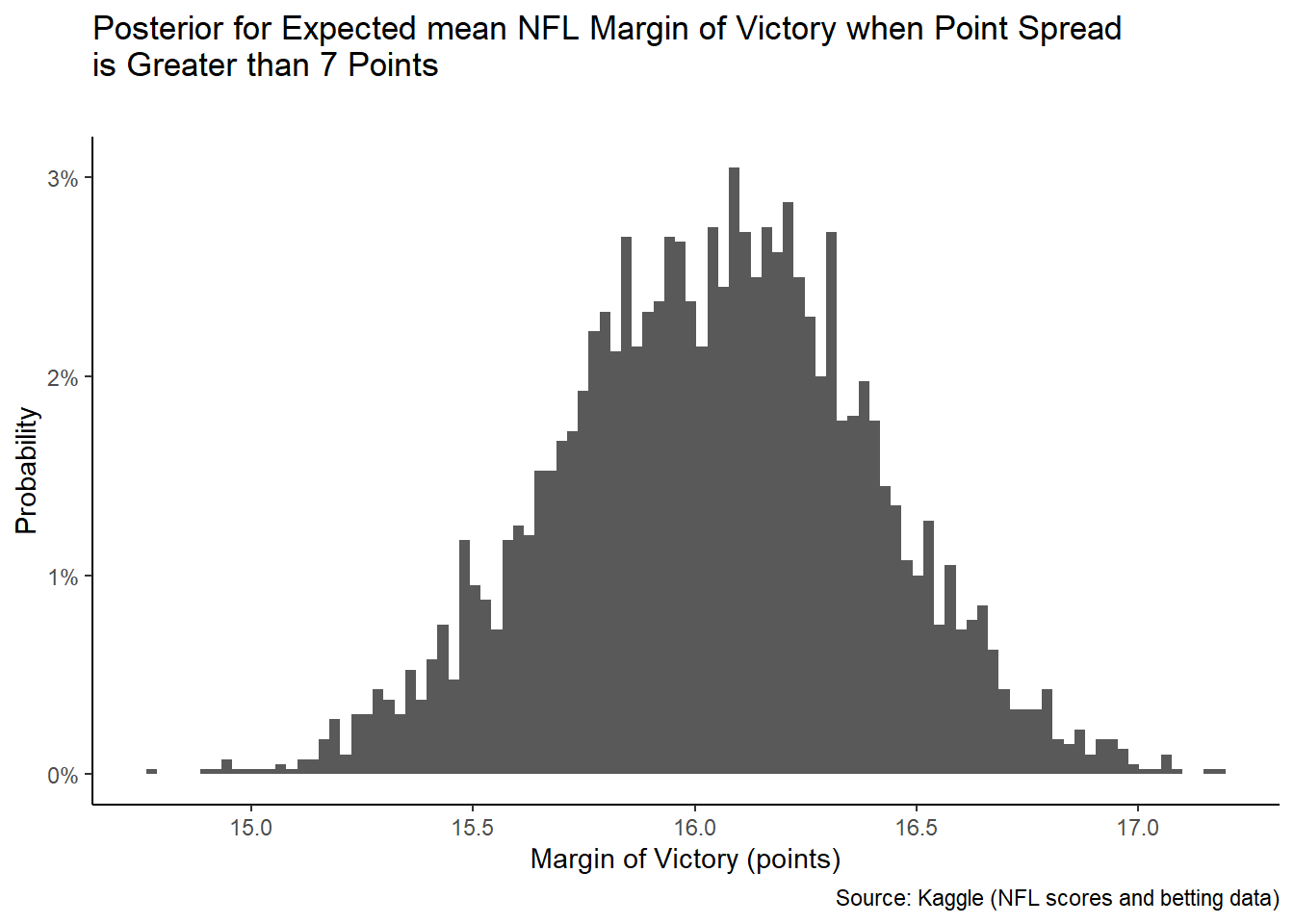
A Bayesian regression model using the stan_glm() function was generated, where the dependent variable is margin of victory and the independent variable is point spread (absolute).

The plots generated from the Bayesian linear model highlight an increasing probable mean margin of victory as the point spread increases. This makes sense, since those matchups are often the case of a far superior opponent versus an inferior opponent. On average, when the spread is greater than 7 points, the mean margin of victory is close to 16 points. Overall, most games are decided by double digits.

What is the expected mean margin of victory?